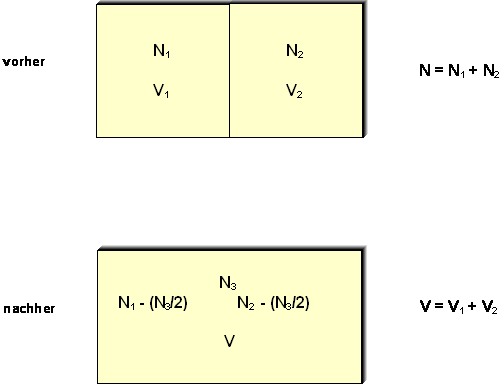
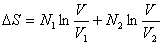Zwei Volumina V₁ und V₂ verschiedener idealer Gase enthalten Moleküle mit den Teilchenzahlen N₁ und N₂, die durch eine mechanisch feste, aber temperaturdurchlässige Wand voneinander getrennt seien. In jedem der beiden Teilsysteme herrsche die gleiche Temperatur T. Die Gesamtzahl der Teilchen sei N = N₁ + N₂. Nun werde die Trennwand entfernt, wobei jeweils ein Molekül der einen Sorte mit einem Molekül der anderen Sorte in eine chemische Reaktion trete, bei der zwei Teilchen entstehen, deren Molekulargewicht gerade gleich dem Mittelwert der beiden Einzelteilchen sei. Die Gesamtzahl der Teilchen ändert sich dabei nicht, im Volumen V befinden sich jetzt lediglich drei verschiedene Molekülsorten, wenn man davon ausgeht, daß eines der beiden ursprünglichen Gase im Überschuß vorhanden war. Auch müssen, nachdem sich ein Gleichgewicht eingestellt hat, nicht alle Teilchen miteinander in Wechselwirkung getreten sein, so daß immer noch Spuren der ursprünglichen Gase vorhanden sind.

 

 

Für die Entropie im Anfangszustand A können wir also schreiben:

 

.

 

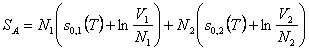wobei s_0,1(T) und s_0,2(T) die Entropien der beiden Gase pro Molekül seien. Da die Reaktion bei konstanter Temperatur T abläuft, lautet die Entropie im Endzustand E:

 

     

 

          

 

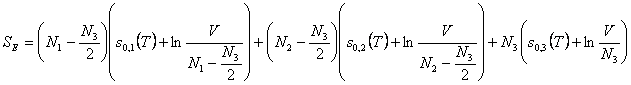
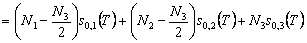
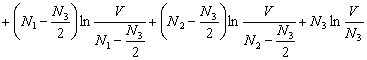
wenn N₃ die Zahl der Teilchen des erhaltenen Reaktionsproduktes ist. Die Entropie pro neu entstandenes Teilchen ist der Mittelwert aus den Entropien jedes der beiden Ausgangsteilchen:

 

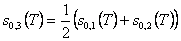
Berechnen wir damit die Entropiedifferenz, die sogenannte Mischungsentropie, so erhalten wir den Ausdruck

                           

          

         

 

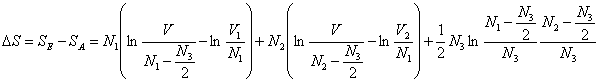
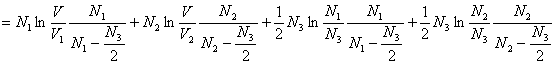
Wegen V > V₁ und V > V₂ sowie N₁ > N₃/2 und N₂ > N₃/2 folgt ΔS > 0, d.h. die Entropie nimmt zu, weil die Durchmischung zweier Gase mit gleichzeitiger Reaktion ein irreversibler Prozeß ist. Für N₃ à 0, d.h. wenn keine chemische Reaktion zwischen den Molekülen stattfindet, erhalten wir wie erwartet den entsprechenden Ausdruck für ein zweikomponentiges ideales Gas: